我院傅星珵老师论文 ”Toward a Unified Geometry Understanding: Riemannian Diffusion Framework for Graph Generation and Prediction”被机器学习领域三大顶会之一的NeurIPS 2025录用。神经信息处理系统大会（NIPS，NeurIPS，Conference and Workshop on Neural Information Processing Systems)，是机器学习、计算神经科学和人工智能领域最权威的会议之一，与 ICML、ICLR 并列为最具影响力的机器学习三大顶级会议，在中国计算机学会（CCF）推荐会议列表中被列为A类会议

  该论文由广西师范大学计算机科学与工程学院/软件学院/人工智能学院、香港科技大学计算机科学与工程系和北京航空航天大学计算机学院合作完成，我院为第一完成单位，通讯作者为我院傅星珵老师。

             单位：

             广西师范大学

             香港科技大学

             北京航空航天大学

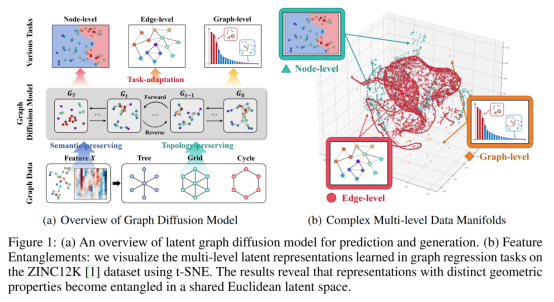
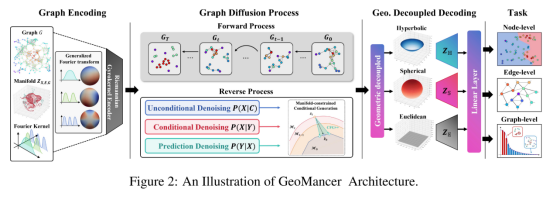
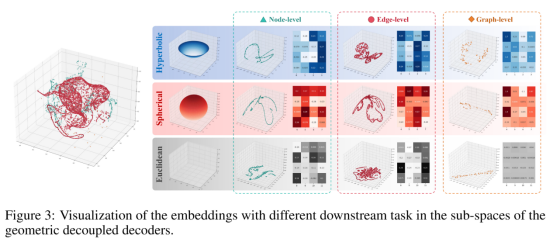
  图扩散模型在学习结构化图数据方面取得了显著进展，并在预测任务中展现出强大的潜力。现有的方法通常将节点、边和图级特征嵌入到统一的潜在空间中，将包括分类和回归在内的预测任务建模为一种条件生成的形式。然而，由于图数据的非欧几里得性质，不同曲率的特征在相同的潜在空间中相互纠缠，无法释放其几何潜力。为了解决这个问题，本文旨在构建一个理想的黎曼扩散模型，以捕捉复杂图数据的不同流形特征并学习其分布。这一目标面临两个挑战：编码过程中由指数映射引起的数值不稳定性和扩散生成过程中的流形偏差。为了解决这些挑战，本文提出GeoMancer：一种用于生成和预测任务的新型黎曼图扩散框架。为缓解数值不稳定性，本文用等距不变黎曼陀螺核方法替代指数映射，并将多级特征解耦到各自特定任务的流形上以学习最优表示。为解决流形偏差问题，本文引入流形约束扩散方法和无条件生成的自引导策略，确保生成的数据与流形特征保持一致。大量实验验证了本文方法的有效性，表明其在各种任务中均表现出色。